特征增强是对数据的进一步修改,我们开始清洗和增强数据。主要涉及的操作有
- 识别数据中的缺失值
- 删除有害数据
- 输入缺失值
- 对数据进行归一化/标准化
1. 识别数据中的缺失值
特征增强的第一种方法是识别数据的缺失值,可以让我们更好的明白如何使用真是世界中的数据。通常,数据因为一些原因,导致数据缺失,不完整。我们需要做的就是识别出数据中的缺失值。并对缺失值进行处理。本文使用皮马印第安人糖尿病预测数据集。这个数据集包含768行数据点,9列特征。预测21岁以上的女性皮马印第安人5年内是否会患糖尿病。数据每列的含义如下:
(1)怀孕次数
(2)口服葡萄糖耐量实验中的2小时血浆葡萄糖浓度
(3)舒张压
(4)三头肌皮褶厚度
(5)2小时血清胰岛素浓度
(6)体重指数
(7)糖尿病家族函数
(8)年龄
(9)类变量(0或1,代表有无糖尿病)
首先我们先来了解一下数据
# 导入探索性数据分析所需的包
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
plt.style.use('fivethirtyeight')
# 添加标题
pima_column_names = ['times_pregnant', 'plasma_glucose_concentration', 'diastolic_blood_pressure', 'triceps_thickness',
'serum_insulin', 'bmi', 'pedigree_function', 'age', 'onset_diabetes']
pima = pd.read_csv('./data/pima.data', names=pima_column_names)
pima.head()
# 计算一下空准确率
pima['onset_diabetes'].value_counts(normalize=True)
# 对plasma_glucose_concentration列绘制两类的直方图
col = 'plasma_glucose_concentration'
plt.hist(pima[pima['onset_diabetes'] == 0][col], 10, alpha=0.5, label='non-diabetes') # 不患糖尿病
plt.hist(pima[pima['onset_diabetes'] == 1][col], 10, alpha=0.5, label='diabetes') # 患糖尿病
plt.legend(loc='upper right')
plt.xlabel(col)
plt.ylabel('Frequency')
plt.title('Histogram of {}'.format(col))
plt.show()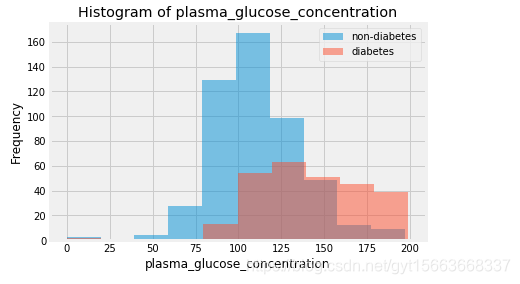
# 线性相关矩阵量化变量间的关系
# 数据相关矩阵的热力图
sns.heatmap(pima.corr())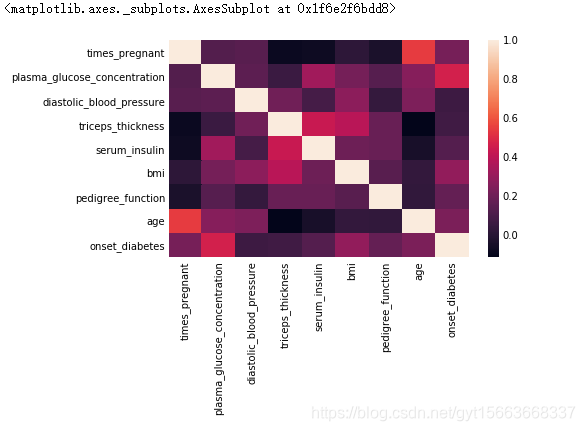
从上面的分析中,我们首先可以得到患者和常人的血糖浓度是有很大的差异的。并且血糖浓度与患者是否患病的相关性很大。下面我们来分析一下数据是否存在缺失值。
# 查看数据中是否存在缺失值
pima.isnull().sum()
从上面的结果我们可以看到并没有缺失值,我们在看一下关于数据的基本描述性统计。
# 查看数据的基本描述性统计
pima.describe()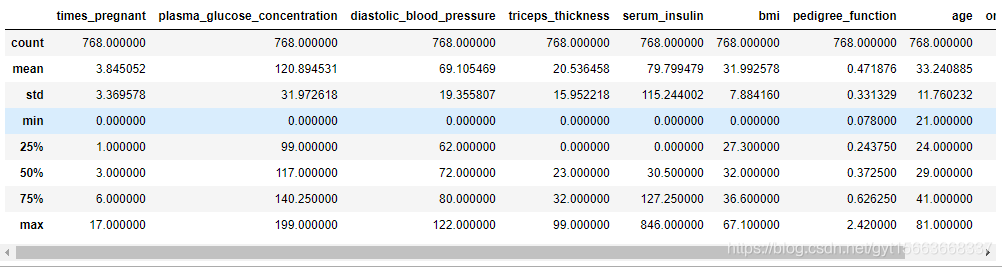
我们可以看到BMI指标的最小值是0.这是有悖于医学常识的。这有可能是缺失或不存在的点都用0填充了。从数据中可以看到,有好几列都是0.但是onset——diabetes中的0代表没有糖尿病,人也可以怀孕0次。所以这两列没有问题,其他的列的缺失值用0填充了。
- plasma_glucose_concentration
- diastolic_blood_pressure
- triceps_thickness
- serum_insulin
- bmi
2. 处理数据中的缺失值
首先,对存在缺失值的列,使用None代替0。然后在查看是否存在缺失值。
# 直接对所有列操作
columns = ['serum_insulin', 'bmi', 'plasma_glucose_concentration', 'diastolic_blood_pressure', 'triceps_thickness']
for col in columns:
pima[col].replace([0], [None], inplace=True)
# 查看缺失值情况
pima.isnull().sum()
(1)删除有害的行
我们首先删除有害的行,然后对删除前后的数据做一个分析,最后应用机器学习算法评估一下当前数据的性能。
删除存在缺失值的数据:
# 删除存在缺失的行
pima_dropped = pima.dropna()
# 检查删除了多少行
num_rows_lost = round(100*(pima.shape[0] - pima_dropped.shape[0]) / float(pima.shape[0]))
print("retained {}% of rows".format(num_rows_lost))retained 49% of rows
数据分析:
# 继续对数据做一下探索性分析
# 未删除数据的空准确率
pima['onset_diabetes'].value_counts(normalize=True)0 0.651042
1 0.348958
Name: onset_diabetes, dtype: float64
# 删除数据后的空准确率
pima_dropped['onset_diabetes'].value_counts(normalize=True)0 0.668367
1 0.331633
Name: onset_diabetes, dtype: float64
从空准确率来看,前后的True和False并无太大的变化。接下来比较一下删除前后的个属性均值。
# 未删除数据的均值
pima.mean()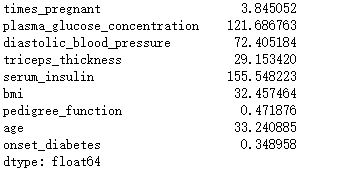
# 删除数据后的均值
pima_dropped.mean()
# 使用条形图进行可视化
# 均值变化百分比条形图
ax = ((pima_dropped.mean() - pima.mean()) / pima.mean()).plot(kind='bar', title='% change in average column values')
ax.set_ylabel('% change')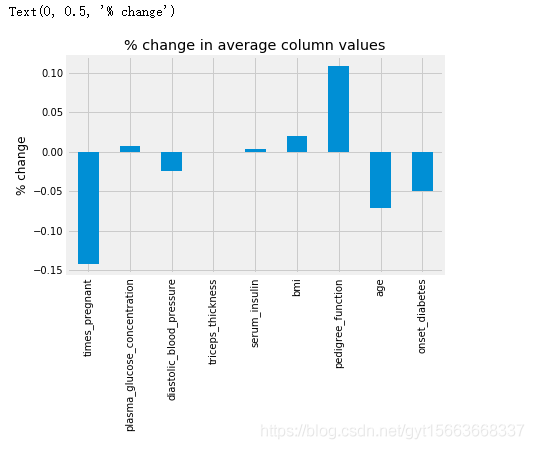
我们可以看到,怀孕次数的均值在删除缺失值后下降了14%,糖尿病血系功能也上升了11%。都变化的比较大。删除行会严重影响数据的形状,所以我们应该保留尽可能多的数据。在我们进行其他操作前,我们使用一个机器学习算法验证一下当前数据情况的模型性能。
评估性能:
# 导入机器学习
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV
# 删除标签数据
X_dropped = pima_dropped.drop('onset_diabetes', axis=1) # 特征
print("leanrning from {} rows".format(X_dropped.shape[0]))
y_dropped = pima_dropped['onset_diabetes'] # 标签
# KNN的模型参数
knn_params = {'n_neighbors': [1, 2, 3, 4, 5, 6, 7]}
# KNN模型
knn = KNeighborsClassifier()
# 使用网格搜索优化
grid = GridSearchCV(knn, knn_params)
grid.fit(X_dropped, y_dropped)
# 输出结果
print(grid.best_score_, grid.best_params_)结果:0.7448979591836735 {‘n_neighbors’: 7}
(2)填充缺失值
首先,我们检查一下缺失值的情况。然后使用sklearn模块的方法填充缺失值,最后在检查缺失值情况,用机器学期方法验证一下模型的性能。
检查缺失值:
# 在此查看缺失值情况
pima.isnull().sum()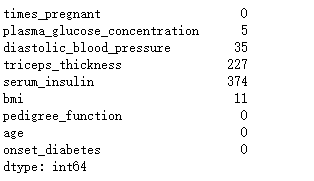
填充缺失值:
# 使用scikit-learn预处理类的Imputer模块
from sklearn.preprocessing import Imputer
# 实例化对象
imputer = Imputer(strategy='mean')
# 创建新对象
pima_imputed = imputer.fit_transform(pima)
# 将得到的ndarray类型转化为DataFrame
pima_imputed = pd.DataFrame(pima_imputed, columns=pima_column_names)
pima_imputed.head()
检查缺失值情况并评估性能:
# 判断是否有缺失值
pima_imputed.isnull().sum()
# 尝试一下填充一些别的值,查看对KNN模型的影响
# 用0填充
pima_zero = pima.fillna(0)
X_zero = pima_zero.drop('onset_diabetes', axis=1)
y_zero = pima_zero['onset_diabetes']
# knn模型参数
knn_params = {'n_neighbors': [1, 2, 3, 4, 5, 6, 7]}
# 网格搜索
grid = GridSearchCV(knn, knn_params)
grid.fit(X_zero, y_zero)
# 输出
print(grid.best_score_, grid.best_params_)结果:0.7330729166666666 {‘n_neighbors’: 6}
3. 标准化和归一化
我们现在要做的是进一步增强机器学习流水线,进行一下探索性数据分析。
impute = Imputer(strategy='mean')
# 填充所有的缺失值
pima_imputed_mean = pd.DataFrame(impute.fit_transform(pima), columns=pima_column_names)
# 画直方图
pima_imputed_mean.hist(figsize=(15, 15))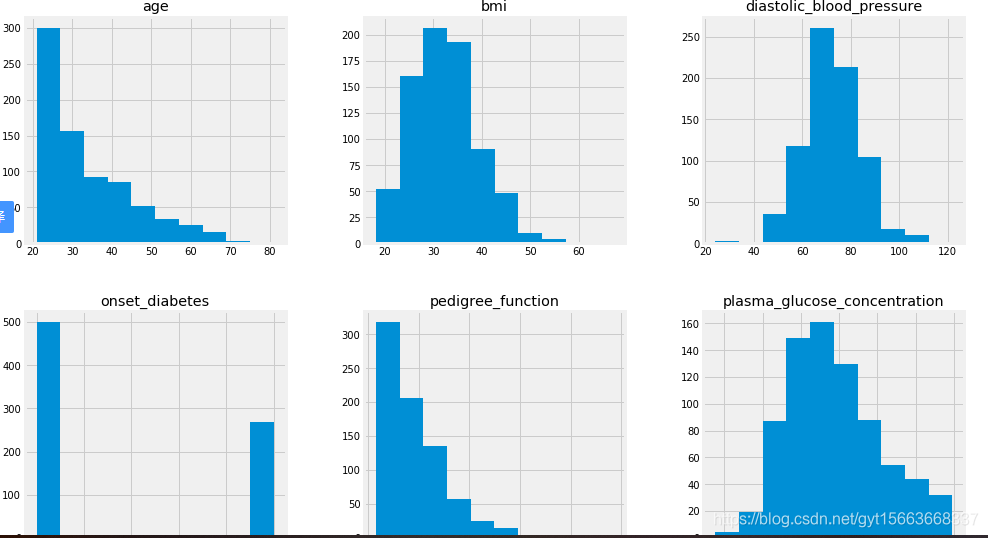
从这分析中可以发现,某些特征数据的尺度不同。有一些机器学习模型受数据尺度的影响很大。因此,我们可以使用某种归一化/标准化操作。
归一化:将行和列对齐并转化为一致的规则。将所有定量列转化为同一个静态范围中的值。
标准化:通过确保所有行和列在机器学习中得到平等对待,让数据的处理保持一致。
(1)z分数标准化
z分数标准化利用了统计学最简单的z分数思想。将特征重新缩放,均值为0、标准差为1。通过缩放特征、统一化均值和方差,可以让机器学习模型达到最优化。公式为
$$
z=\frac{x-\mu }{\sigma }
$$
其中$\mu$为均值,$\sigma$为标准差。
# 取此列均值
mu = pima['plasma_glucose_concentration'].mean()
# 取此列标准差
sigma = pima['plasma_glucose_concentration'].std()
# 对每个值计算z分数
print(((pima['plasma_glucose_concentration'] - mu) / sigma).head())
# 使用内置的z分数归一化
from sklearn.preprocessing import StandardScaler
# 用z分数标准化
scaler = StandardScaler()
glucose_z_score_standardized = scaler.fit_transform(pima[['plasma_glucose_concentration']])
# 直方图
ax = pd.Series(glucose_z_score_standardized.reshape(-1,)).hist()
ax.set_title('Distribution of plasma_glucose_concentration after Z Score Scaling')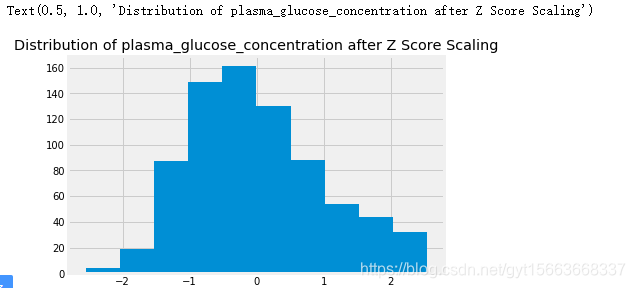
# 将z分数标准化插入到机器学习流水线上
knn_params = {'imputer__strategy': ['mean', 'median'], 'classify__n_neighbors': [1, 2, 3, 4, 5, 6, 7]}
mean_impute_standardize = Pipeline([('imputer', Imputer()), ('standardize', StandardScaler()), ('classify', knn)])
X = pima.drop('onset_diabetes', axis=1)
y = pima['onset_diabetes']
grid = GridSearchCV(mean_impute_standardize, knn_params)
grid.fit(X, y)
print(grid.best_score_, grid.best_params_)结果:0.7421875 {‘classify__n_neighbors’: 7, ‘imputer__strategy’: ‘median’}
(2)min-max标准化
$$
m=\frac{x-x_{min} }{x_{max}-x_{min}}
$$
其中,$x_{min}$为该列最小值,$x_{max}$为该列最大值。
标准化
# 导入sklearn模块
from sklearn.preprocessing import MinMaxScaler
# 实例化
min_max = MinMaxScaler()
# min-max标准化
pima_min_maxed = pd.DataFrame(min_max.fit_transform(pima_imputed), columns=pima_column_names)
# 得到描述性统计
pima_min_maxed.describe()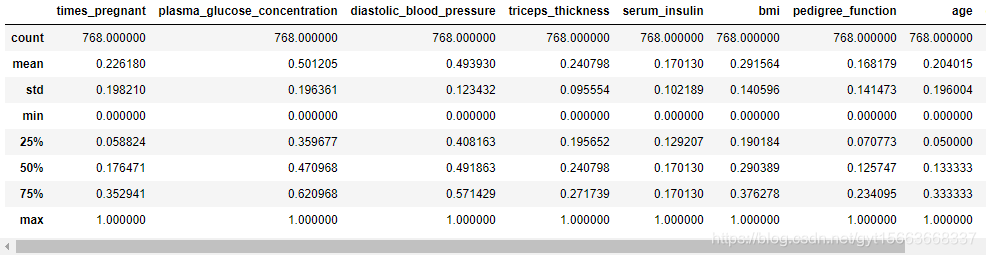
评估性能
knn_params = {'imputer__strategy': ['mean', 'median'], 'classify__n_neighbors': [1, 2, 3, 4, 5, 6, 6]}
mean_impute_standardize = Pipeline([('imputer', Imputer()), ('standardize', MinMaxScaler()), ('classify', knn)])
X = pima.drop('onset_diabetes', axis=1)
y = pima['onset_diabetes']
grid = GridSearchCV(mean_impute_standardize, knn_params)
grid.fit(X, y)
print(grid.best_score_, grid.best_params_)结果:0.74609375 {‘classify__n_neighbors’: 4, ‘imputer__strategy’: ‘mean’}
(3)行归一化
行归一化是针对行进行操作的,保证每行有单位范数,也就是每行的向量长度相同。
$$
\left | x \right |=\sqrt{(x_{1}^{2}+x_{2}^{2}+…+x_{n}^{2})}
$$
归一化
# 引入行归一化
from sklearn.preprocessing import Normalizer
# 实例化
normalize = Normalizer()
pima_normalized = pd.DataFrame(normalize.fit_transform(pima_imputed), columns=pima_column_names)
# 行归一化后矩阵的平均范数
np.sqrt((pima_normalized**2).sum(axis=1)).mean()结果:1.0
评估性能
knn_params = {'imputer__strategy': ['mean', 'median'], 'classify__n_neighbors': [1, 2, 3, 4, 5, 6, 6]}
mean_impute_standardize = Pipeline([('imputer', Imputer()), ('normalize', Normalizer()), ('classify', knn)])
X = pima.drop('onset_diabetes', axis=1)
y = pima['onset_diabetes']
grid = GridSearchCV(mean_impute_standardize, knn_params)
grid.fit(X, y)
print(grid.best_score_, grid.best_params_)结果:0.6822916666666666 {‘classify__n_neighbors’: 6, ‘imputer__strategy’: ‘mean’}
从本章的学习中,我们处理了数据中的缺失值,并使用标准化/归一化的方法继续处理数据。然后我们评估了性能。得到的结果是使用均值填充数据,然后用min-max标准化处理出具。得到0.7461的准确率。注意,虽然这个数据比删除存在缺失值的数据准确率没有高很多。但是这是使用全部数据训练的结果。更具有一般化。泛化性能将更好。




